Gringarten and Witherspoon Solution for Fractured Aquifers with a Single Vertical Plane Fracture

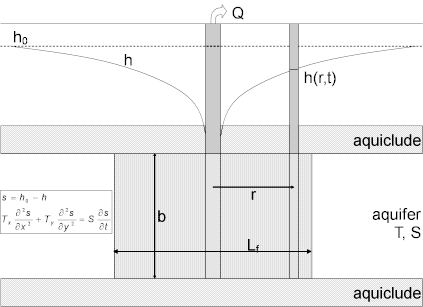
A mathematical solution by Gringarten and Witherspoon (1972) is useful for determining the hydraulic properties (hydraulic conductivity, specific storage, hydraulic conductivity anisotropy and fracture length) of fractured aquifers with a single vertical plane fracture intersecting the pumped well. Analysis involves matching the solution to drawdown data collected during a pumping test. The solution estimates hydraulic conductivity anisotropy in a horizontal (x-y) plane.

AQTESOLV provides two configurations for simulating a vertical fracture using the Gringarten and Witherspoon (1972) solution: uniform flux and infinite conductivity. Select the appropriate condition when you choose a solution.

You are not restricted to constant-rate tests with the Gringarten and Witherspoon solution. AQTESOLV incorporates the principle of superposition in time to simulate variable-rate and recovery tests with this method.

The early-time response of a pumped well intersecting a vertical fracture has a distinct signature that you can diagnose with a linear flow plot.

Due to anisotropy, use of a distance-drawdown plot with the Gringarten and Witherspoon solution is limited to wells located on the x-coordinate axis.

Assumptions

• aquifer has infinite areal extent
• aquifer has uniform thickness
• aquifer potentiometric surface is initially horizontal
• pumping and observation wells are fully penetrating
• fractured aquifer represented by anisotropic nonleaky confined system with a single plane vertical fracture that fully penetrates aquifer
• flow is unsteady
• water is released instantaneously from storage with decline of hydraulic head
• diameter of control well is very small so that storage in the well can be neglected

Equations

The following equation by Gringarten and Witherspoon (1972) predicts drawdown in a nonleaky confined aquifer with a uniform-flux vertical fracture:

$$s=\frac{Q}{4\pi \sqrt{T_x{T}_y}}\frac{\sqrt{\pi }}{2}{\int }_0^{t_D}\left(\mathrm{erf}\frac{1-x_D}{2\sqrt{\tau }}+\mathrm{erf}\frac{1+x_D}{2\sqrt{\tau }}\right)·e^{-y_D^2{T}_x/\left(4\tau T_y\right)}\frac{d\tau }{\sqrt{\tau }}\text{(1)}$$ $$x_D=x/x_f\text{(2)}$$ $$y_D=y/x_f\text{(3)}$$ $$t_D=\frac{T_{x}t}{S{x}_f^2}\text{(4)}$$ $$s_D=\frac{4\pi \sqrt{T_x{T}_y}}{Q}s\text{(5)}$$

where

• $\mathrm{erf}\left(\right)$ is the error function
• $Q$ is pumping rate [L³/T]
• $s$ is drawdown [L]
• $S$ is storativity ($=S_{s}b$) [dimensionless]
• $t$ is elapsed time since start of pumping [T]
• $T_x$ is transmissivity in x direction ($=K_{x}b$) [L²/T]
• $T_y$ is transmissivity in y direction ($=K_{y}b$) [L²/T]
• $\tau$ is a variable of integration
• $x$ is distance in x direction [L]
• $x_f$ is half-length of fracture in x direction [L]
• $y$ is distance in y direction [L]

Notes

1. Equations (1) through (5) assume a uniform-flux condition along the fracture.
2. Gringarten, Ramey and Raghavan (1974) found that equations (1) through (5) could be used to predict drawdown in an infinite-conductivity fracture by simply using $x_D$ = 0.732 to compute drawdown in the pumped well.

Data Requirements

• pumping and observation well locations
• pumping rate(s)
• observation well measurements (time and displacement)
• saturated thickness
• length of fracture

Solution Options

• variable pumping rates
• multiple pumping wells
• multiple observation wells
• boundaries

Estimated Parameters

• $K_x$ (hydraulic conductivity in x direction)
• $S_s$ (specific storage)
• $K_y/K_x$ (hydraulic conductivity anisotropy ratio)
• $L_f$ (length of fracture)

Curve Matching Tips

• Use linear flow plots to help diagnose linear flow.
• Match the Cooper and Jacob (1946) solution to late-time data to obtain preliminary estimates of aquifer properties.
• Choose Match>Visual to perform visual curve matching using the procedure for type curve solutions.
• Use active type curves for more effective visual matching with variable-rate pumping tests.
• Select values of $K_y/K_x$ from the Family and Curve drop-down lists on the toolbar.
• Use parameter tweaking to perform visual curve matching and sensitivity analysis.
• Perform visual curve matching prior to automatic estimation to obtain reasonable starting values for the aquifer properties.

Benchmark

References

Gringarten, A.C. and P.A. Witherspoon, 1972. A method of analyzing pump test data from fractured aquifers, Int. Soc. Rock Mechanics and Int. Assoc. Eng. Geol., Proc. Symp. Rock Mechanics, Stuttgart, vol. 3-B, pp. 1-9.