Cooley and Case Solution for Leaky Confined Aquifers

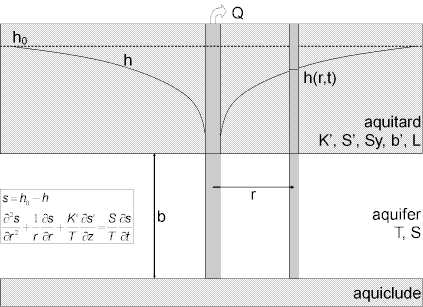
A mathematical solution by Cooley and Case (1973) is useful for determining the hydraulic properties (transmissivity, storativity and leakage parameters) of a leaky confined aquifer with a water-table aquitard. Analysis involves matching the Cooley and Case solution to drawdown data collected during a constant- or variable-rate pumping test.

You are not restricted to constant-rate tests with the Cooley and Case solution. AQTESOLV incorporates the principle of superposition in time to simulate variable-rate and recovery tests with this method.

Assumptions

• aquifer has infinite areal extent
• aquifer is homogeneous, isotropic and of uniform thickness
• potentiometric surface is initially horizontal
• aquifer is confined
• flow is unsteady
• wells are fully penetrating
• water is released instantaneously from storage with decline of hydraulic head
• diameter of control well is very small so that storage in the well can be neglected
• confining bed has infinite areal extent, uniform vertical hydraulic conductivity, storage coefficient, specific yield and thickness
• flow is vertical in the aquitard

Equations

Cooley and Case (1973) derived a solution for unsteady flow to a fully penetrating well in a homogeneous, isotropic leaky confined aquifer overlain by a water-table aquitard. The Laplace transform solution is as follows:

$${\overline{s}}_D=\frac{2K_0\left(x\right)}{p}\text{ (1)}$$ $$x=\sqrt{p+{\overline{q}}_D}\text{ (2)}$$ $${\overline{q}}_D=4\sqrt{p}\beta \coth \left(\frac{4\sqrt{p}\beta }{{\left(r/B\right)}^2}\right)+\left[p{\mathrm{sech}}^2\left(\frac{4\sqrt{p}\beta }{{\left(r/B\right)}^2}\right)\right]\times$$ $${\left[p\frac{L/b^{\prime }}{{\left(r/B\right)}^2}+\frac{{\left(r/B\right)}^2}{16{\beta }^2}\frac{S^{\prime }}{S_y}+\frac{\sqrt{p}}{4\beta }\tanh \left(\frac{4\sqrt{p}\beta }{{\left(r/B\right)}^2}\right)\right]}^{\mathrm{-1}}\text{ (3)}$$ $$B=\sqrt{\frac{T\left(b^{\prime }+L\right)}{K^{\prime }}}\text{ (3)}$$ $$\beta =\frac{r}{4}\sqrt{\frac{K^{\prime }{S}^{\prime }}{b^{\prime }TS}}\text{ (5)}$$ $$t_D=\frac{Tt}{S{r}^2}\text{ (6)}$$ $$s_D=\frac{4\pi T}{Q}s\text{ (7)}$$

where

• $b^{\prime }$ is thickness of aquitard [L]
• $K^{\prime }$ is vertical hydraulic conductivity of aquitard [L/T]
• $K_0$ is modified Bessel function of second kind, order zero
• $L$ is height of capillary fringe [L]
• $p$ is Laplace transform variable
• $Q$ is pumping rate [L³/T]
• $r$ is radial distance from pumping well to observation well [L]
• $s$ is drawdown [L]
• $S$ is storativity [dimensionless]
• $S^{\prime }$ is storativity of aquitard [dimensionless]
• $S_y$ is specific yield of aquitard [dimensionless]
• $t$ is elapsed time since start of pumping [T]
• $T$ is transmissivity [L²/T]

Data Requirements

• pumping and observation well locations
• pumping rate(s)
• observation well measurements (time and displacement)

Solution Options

• constant or variable pumping rate with recovery
• multiple pumping wells
• multiple observation wells
• boundaries

Estimated Parameters

• $T$ (transmissivity)
• $S$ (storativity)
• $r/B$ (leakage parameter)
• $\beta$ (leakage parameter)
• $S^{\prime }/S_y$ (storage ratio in aquitard)
• $L/b^{\prime }$ (dimensionless height of capillary fringe)

The Report view shows aquitard properties, $K\prime /b\prime$ and $K\prime$, computed from the leakage parameter, $r/B$.

Curve Matching Tips

• Use the Cooper and Jacob (1946) solution to obtain preliminary estimates of aquifer properties.
• Choose Match>Visual to perform visual curve matching using the procedure for type curve solutions.
• Use active type curves for more effective visual matching with variable-rate pumping tests.
• Select values of $r/B$ and $\beta$ from the Family and Curve drop-down lists on the toolbar.
• Use parameter tweaking to perform visual curve matching and sensitivity analysis.
• Perform visual curve matching prior to automatic estimation to obtain reasonable starting values for the aquifer properties.

References

Cooley, R.L. and C.M. Case, 1973. Effect of a water table aquitard on drawdown in an underlying pumped aquifer, Water Resources Research, vol. 9, no. 2, pp. 434-447.