Dougherty and Babu Slug Test Solution for Confined Aquifers
Related Solution Methods
Additional Topics
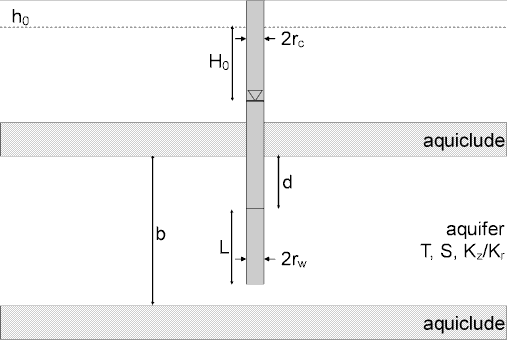
Dougherty and Babu (1984) presented a mathematical solution for determining the hydraulic properties of nonleaky confined aquifers from an overdamped slug test. The solution accounts for wellbore skin as well as hydraulic conductivity anisotropy (Moench 1988). Analysis involves matching a type curve solution to water-level displacement data from the control well and observation wells.
The following Laplace transform solution evaluates dimensionless drawdown in the control well:
The Laplace transform solution for dimensionless drawdown in a piezometer is as follows:
The Laplace transform solution for dimensionless drawdown in an observation well is given by the following equation:
where
- is aquifer thickness [L]
- is the depth to the top of control well screen [L]
- is the depth to the top of observation well screen [L]
- is displacement at time [L]
- is initial displacement at [L]
- is radial (horizontal) hydraulic conductivity [L/T]
- is vertical hydraulic conductivity [L/T]
- is modified Bessel function of second kind, order
- is the depth to the bottom of control well screen [L]
- is the depth to the bottom of observation well screen [L]
- is the Laplace transform variable
- is radial distance from control well to observation well [L]
- is casing radius [L]
- is well radius [L]
- is storativity [dimensionless]
- is wellbore skin factor [dimensionless]
- is elapsed time since initiation of test [T]
- is transmissivity [L²/T]
- is piezometer depth [L]
Note that is typically taken as the borehole radius (i.e., extending to the outer radius of the filter pack) when the filter pack is expected to be more conductive than the aquifer.
In a confined aquifer with no wellbore skin, the Dougherty and Babu slug test solution is equivalent to Cooper et al. (1967) for fully penetrating wells and the KGS Model for partially penetrating wells.
The implementation of wellbore skin in the Dougherty and Babu solution differs from the KGS Model. Dougherty and Babu assumes an infinitesimal skin thickness while the KGS Model has a finite-thickness skin.
Assumptions
The following assumptions apply to the use of the Dougherty and Babu solution:
- aquifer has infinite areal extent
- aquifer is homogeneous and of uniform thickness
- aquifer potentiometric surface is initially horizontal
- wells are fully or partially penetrating
- a volume of water, V, is injected or discharged instantaneously from the control well
- flow to control well is horizontal
- aquifer is nonleaky confined
- flow is unsteady
- water is released instantaneously from storage with decline of hydraulic head
Solution
Options
AQTESOLV provides the following options for the Dougherty and Babu solution:
- partially penetrating wells
- hydraulic conductivity anisotropy
- wellbore skin effect
- observation wells
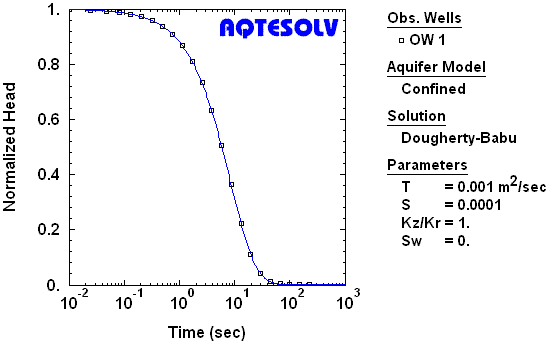
Benchmark
References
Dougherty, D.E and D.K. Babu, 1984. Flow to a partially penetrating well in a double-porosity reservoir, Water Resources Research, vol. 20, no. 8, pp. 1116-1122.