Hvorslev Slug Test Solution for Confined Aquifers
Related Solution Methods
Additional Topics
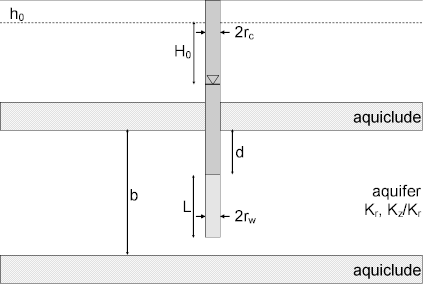
 A mathematical solution by Hvorslev (1951) is useful for determining the hydraulic conductivity () of nonleaky confined aquifers. Analysis involves matching a straight line to water-level displacement data collected during an overdamped slug test.
A mathematical solution by Hvorslev (1951) is useful for determining the hydraulic conductivity () of nonleaky confined aquifers. Analysis involves matching a straight line to water-level displacement data collected during an overdamped slug test.
Danish-American geotechnical engineer Mikael Juul Hvorslev (1895-1989) introduced an approximate mathematical model for the interpretation of overdamped slug tests in partially penetrating wells or piezometers. Hvorslev's transient solution omits storativity of the formation and assumes quasi-steady-state flow between the control well and the tested formation. Zlotnik (1994) introduced an equivalent well radius for partially penetrating wells to incorporate hydraulic conductivity anisotropy.
Hvorslev's equation for a partially penetrating well or piezometer not in contact with an impermable boundary is as follows:
where
- is displacement at time [L]
- is initial displacement at [L]
- is radial (horizontal) hydraulic conductivity [L/T]
- is vertical hydraulic conductivity [L/T]
- is screen length [L]
- is nominal casing radius [L]
- is well radius [L]
- is elapsed time since initiation of the test [T]
Note that is typically taken as the borehole radius (i.e., extending to the outer radius of the filter pack) when the filter pack is expected to be more conductive than the aquifer.
For a well abutting a confining unit, Equation 1 is replaced by the following expression:
In the case of a fully penetrating well, the following relationship is used instead of Equation 1 (Butler 1998):
While intended for confined aquifers, the Hvorslev method can yield appropriate estimates of for overdamped tests in unconfined aquifers as long as the well screen is not too close to the water table (more information).
AQTESOLV includes recommended head ranges (Butler 1998) for the Hvorslev solution that can reduce ambiguity when interpreting response data with a concave upward appearance.
Assumptions
The following assumptions apply to the use of the Hvorslev slug test method:
- aquifer has infinite areal extent
- aquifer is homogeneous and of uniform thickness
- aquifer potentiometric surface is initially horizontal
- control well is fully or partially penetrating
- a volume of water, V, is injected or discharged instantaneously from the control well
- aquifer is confined or unconfined
- flow is steady
Solution
Options
AQTESOLV provides the following options for the Hvorslev method for overdamped slug tests:
- partially penetrating wells
- correction for gravel pack porosity
- hydraulic conductivity anisotropy
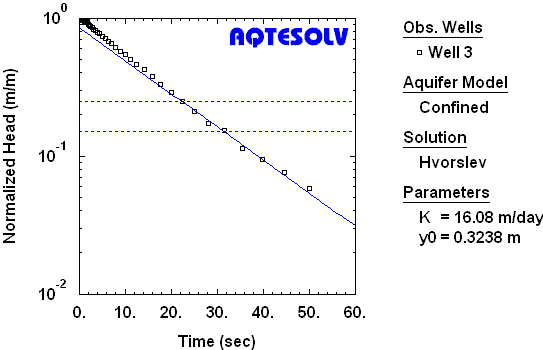
Benchmark
References
Hvorslev, M.J., 1951. Time Lag and Soil Permeability in Ground-Water Observations, Bull. No. 36, Waterways Exper. Sta. Corps of Engrs, U.S. Army, Vicksburg, Mississippi, pp. 1-50.