Butler Solution for Confined Aquifers with Nonuniform Properties
- Assumptions
- Equations
- Data requirements
- Solution options
- Estimated parameters
- Curve matching tips
- References
Related Solution Methods
Additional Topics
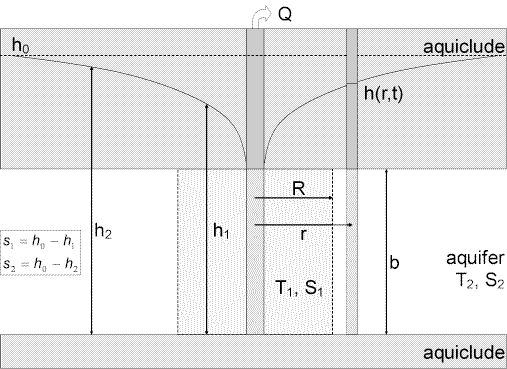
 A mathematical solution by Butler (1988) is useful for determining the hydraulic properties (transmissivity and storativity of two zones) of nonleaky confined aquifers with nonuniform properties.
A mathematical solution by Butler (1988) is useful for determining the hydraulic properties (transmissivity and storativity of two zones) of nonleaky confined aquifers with nonuniform properties.
The solution assumes the pumping well is located at the center of a disk embedded within an infinite matrix. Hydraulic properties are assumed uniform within each zone (disk and matrix), but may differ between the two zones. The solution assumes a line source for the pumped well and therefore neglects wellbore storage.
Analysis involves matching the Butler solution to drawdown data collected during a pumping test.
You are not restricted to constant-rate tests with the Butler solution. Using the principle of superposition in time, AQTESOLV can simulate variable-rate and recovery tests with this method.
Assumptions
- aquifer has infinite areal extent
- aquifer is heterogeneous with a disk embedded within a matrix
- control well is fully penetrating
- flow to control well is horizontal
- aquifer is confined
- flow is unsteady
- water is released instantaneously from storage with decline of hydraulic head
- diameter of control well is very small so that storage in the well can be neglected
Equations
Butler (1988) derived a solution for unsteady flow to a fully penetrating line source in a heterogeneous, isotropic confined aquifer. The solution assumes the pumping well is located at the center of a disk of radius embedded within an infinite matrix. The Laplace transform solution is as follows:
where
- is modified Bessel function of first kind, order i
- is modified Bessel function of second kind, order i
- is Laplace transform variable
- is pumping rate [L³/T]
- is radial distance from pumping well to observation well [L]
- is radial distance to disk-matrix interface [L]
- is drawdown in the disk [L]
- is drawdown in the matrix [L]
- is storativity in the disk [dimensionless]
- is storativity in the matrix [dimensionless]
- is elapsed time since start of pumping [T]
- is transmissivity in the disk [L²/T]
- is transmissivity in the matrix [L²/T]
Data Requirements
- pumping and observation well locations
- pumping rate(s)
- observation well measurements (time and displacement)
Solution Options
- variable pumping rates
- multiple observation wells
Estimated Parameters
AQTESOLV provides visual and automatic methods for matching the Butler method to data from pumping tests and recovery tests. The estimated aquifer properties are as follows:
- (transmissivity in disk)
- (storativity in disk)
- (transmissivity in matrix)
- (storativity in matrix)
- (radial distance to disk-matrix interface)
Curve Matching Tips
- Match the Cooper and Jacob (1946) solution to late-time data to obtain preliminary estimates of aquifer properties.
- Choose Match>Visual to perform visual curve matching using the procedure for type curve solutions.
- Use active type curves for more effective visual matching with variable-rate pumping tests.
- Use parameter tweaking to perform visual curve matching and sensitivity analysis.
- Perform visual curve matching prior to automatic estimation to obtain reasonable starting values for the aquifer properties.
References
Butler, J.J., Jr., 1988. Pumping tests in nonuniform aquifers—the radially symmetric case, Journal of Hydrology, vol. 101, pp. 15-30.