Dougherty and Babu Solution for Confined Aquifers
- Assumptions
- Equations
- Data requirements
- Solution options
- Estimated parameters
- Curve matching tips
- Benchmark
- References
Related Solution Methods
Additional Topics
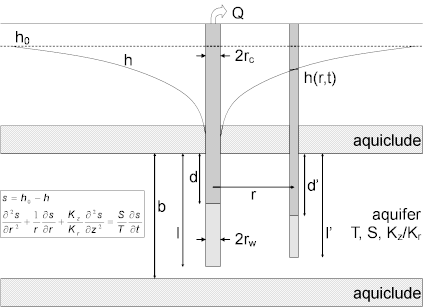
Dougherty and Babu (1984) developed a mathematical solution for determining the hydraulic properties of a nonleaky confined aquifer. Their solution extends the familiar Theis/Hantush method, which assumes a well of infinitessimal diameter, to include the effects of wellbore storage and wellbore skin in a finite-diameter pumping well. Analysis involves matching curves for the Dougherty and Babu solution to drawdown data collected during a pumping test.
Assumptions
- aquifer has infinite areal extent
- aquifer is homogeneous, anisotropic and of uniform thickness
- control well is fully or partially penetrating
- flow to control well is horizontal when the control well is fully penetrating
- aquifer is nonleaky confined
- flow is unsteady
- water is released instantaneously from storage with decline of hydraulic head
Equations
The Dougherty and Babu solution models drawdown in and around a finite-diameter, partially penetrating pumping well discharging from a nonleaky confined aquifer. Their solution includes wellbore storage and wellbore skin effects at the pumped well. Moench (1988) extended the method to account for anisotropic conditions. The following Laplace transform solution evaluates dimensionless drawdown in the pumped well:
The Laplace transform solution for dimensionless drawdown in a piezometer is as follows:
The Laplace transform solution for dimensionless drawdown in an observation well is given by the following equation:
where
- is aquifer thickness [L]
- is the depth to the top of pumping well screen [L]
- is the depth to the top of observation well screen [L]
- is hydraulic head at time [L]
- is initial hydraulic head [L]
- is radial (horizontal) hydraulic conductivity [L/T]
- is vertical hydraulic conductivity [L/T]
- is modified Bessel function of second kind, order
- is the depth to the bottom of pumping well screen [L]
- is the depth to the bottom of observation well screen [L]
- is the Laplace transform variable
- is pumping rate [L³/T]
- is radial distance from pumping well to observation well [L]
- is casing radius [L]
- is well radius [L]
- is drawdown [L]
- is storativity [dimensionless]
- is wellbore skin factor [dimensionless]
- is elapsed time since start of pumping [T]
- is transmissivity [L²/T]
- is piezometer depth [L]
Data Requirements
- pumping and observation well locations
- pumping rate(s)
- observation well measurements (time and displacement)
- casing radius and wellbore radius for pumping well(s)
- downhole equipment radius (optional)
- partial penetration depths
- saturated thickness
- hydraulic conductivity anisotropy ratio
Solution Options
- large-diameter pumping wells
- variable pumping rates
- multiple pumping wells
- multiple observation wells
- partially penetrating wells
- boundaries
Estimated Parameters
AQTESOLV provides visual and automatic methods for matching the Dougherty and Babu method to data from pumping tests and recovery tests. The estimated aquifer properties are as follows:
- (transmissivity)
- (storativity)
- (hydraulic conductivity anisotropy ratio)
- (dimensionless wellbore skin factor)
- (well radius)
- (nominal casing radius)
Curve Matching Tips
- Use radial flow plots to help diagnose wellbore storage.
- Match the Cooper and Jacob (1946) solution to late-time data to obtain preliminary estimates of aquifer properties.
- Match early-time data affected by wellbore storage by adjusting with parameter tweaking.
- If you estimate for the test well, the estimated value replaces the nominal casing radius and AQTESOLV still performs the correction for downhole equipment.
- Choose Match>Visual to perform visual curve matching using the procedure for type curve solutions.
- Use active type curves for more effective visual matching with variable-rate pumping tests.
- Select values of from the Family and Curve drop-down lists on the toolbar.
- Use parameter tweaking to perform visual curve matching and sensitivity analysis.
- Perform visual curve matching prior to automatic estimation to obtain reasonable starting values for the aquifer properties.
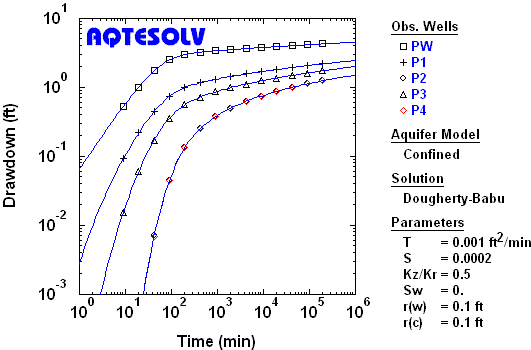
Benchmark
References
Dougherty, D.E and D.K. Babu, 1984. Flow to a partially penetrating well in a double-porosity reservoir, Water Resources Research, vol. 20, no. 8, pp. 1116-1122.
Moench, A.F., 1988. The response of partially penetrating wells to pumpage from double-porosity aquifers, Proceedings of the International Conference on Fluid Flow in Fractured Rocks, Atlanta, GA, May 16-18, 1988.