Hantush and Jacob Step Drawdown Test Solution for Leaky Confined Aquifers

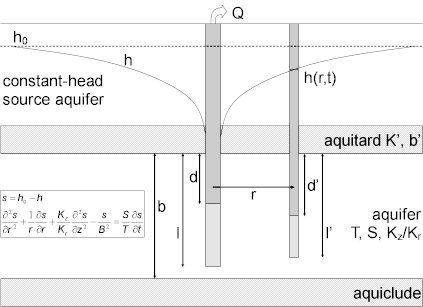
Hantush and Jacob (1955) developed a mathematical solution for determining the hydraulic properties of leaky confined aquifers. Hantush (1961a, b) subsequently introduced equations for partially penetrating wells.

For step-drawdown tests, the Hantush and Jacob solution can be modified to include linear and nonlinear well losses in the pumping well (Jacob 1947; Rorabaugh 1953; Ramey 1982). Analysis involves matching a curve to drawdown data collected during a step-drawdown test.

Assumptions

• aquifer has infinite areal extent
• aquifer is homogeneous, isotropic and of uniform thickness
• pumping well is fully or partially penetrating
• aquifer is leaky confined
• flow is unsteady
• water is released instantaneously from storage with decline of hydraulic head
• diameter of pumping well is very small so that storage in the well can be neglected
• aquitards have infinite areal extent, uniform vertical hydraulic conductivity and uniform thickness
• aquitards are overlain or underlain by an infinite constant-head plane source
• aquitards are incompressible (no storage)
• flow in the aquitards is vertical

Equations

The Hantush and Jacob model for a partially penetrating pumping well in an anisotropic leaky confined aquifer, adapted for step-drawdown tests to include linear and nonlinear well loss, is given by the following equation:

$$s_{\mathrm{w}}=\frac{Q}{4\pi T}[\mathrm{w}\left(u,r/B\right)+\frac{2b^2}{{\pi }^2{\left(l-d\right)}^2}\sum _{n=1}^{\infty }\frac{1}{n^2}{\left(\sin \left(\frac{n\pi l}{b}\right)-\sin \left(\frac{n\pi d}{b}\right)\right)}^2·\mathrm{w}\left(u\mathrm{,}\sqrt{{(r/B)}^2+K_z/K_r{\left(\frac{n\pi r_w}{b}\right)}^2}\right)+\frac{2b}{\left(l-d\right)}{S}_w]+C{Q}^P\text{(1)}$$ $$u=\frac{r_w^{2}S}{4Tt}\text{(2)}$$

where

• $b$ is aquifer thickness [L]
• $C$ is nonlinear well loss coefficient [T^P/L^3P-1]
• $d$ is the depth to the top of pumping well screen [L]
• $K_r$ is the radial (horizontal) hydraulic conductivity [L/T]
• $K_z$ is the vertical hydraulic conductivity [L/T]
• $l$ is the depth to the bottom of pumping well screen [L]
• $Q$ is pumping rate [L³/T]
• $r_{\mathrm{w}}$ is well radius [L]
• $s_{\mathrm{w}}$ is drawdown in the pumped well [L]
• $S$ is storativity [dimensionless]
• $S_{\mathrm{w}}$ is wellbore skin factor [dimensionless]
• $t$ is elapsed time since start of pumping [T]
• $T$ is transmissivity [L²/T]
• $\text{w}(u,\beta )$ is the Hantush and Jacob well function for leaky confined aquifers [dimensionless]

The exponent, $P$, in the nonlinear well loss term, $C{Q}^P$, is generally taken to be 2 as originally proposed by Jacob (1947); however, Rorabaugh (1953) postulated that $P$ may range between 1.5 and 3.5.

Data Requirements

• pumping and observation well locations
• pumping rate(s)
• observation well measurements (time and displacement)
• partial penetration depths (optional)
• saturated thickness (for partially penetrating wells)
• hydraulic conductivity anisotropy ratio (for partially penetrating wells)

Solution Options

• variable pumping rates
• multiple pumping wells
• multiple observation wells
• partially penetrating pumping and observation wells
• boundaries

Estimated Parameters

• $T$ (transmissivity)
• $S$ (storativity)
• $r/B$ (leakage parameter)
• $S_w$ (wellbore skin factor)
• $C$ (nonlinear well loss coefficient)
• $P$ (nonlinear well loss exponent)

Curve Matching Tips

• Use the Cooper and Jacob (1946) solution to obtain preliminary estimates of aquifer properties.
• Choose Match>Visual to perform visual curve matching using the procedure for type curve solutions.
• Use active type curves for more effective visual matching with variable-rate pumping tests.
• Select values of $r/B$ from the Family and Curve drop-down lists on the toolbar.
• Use parameter tweaking to perform visual curve matching and sensitivity analysis.
• Perform visual curve matching prior to automatic estimation to obtain reasonable starting values for the aquifer properties.
• Due to correlation in the equations between $S$ (storativity) and $S_w$ (wellbore skin factor), estimate either $S$ or $S_w$ for a single-well test but not both as the same time.

Example

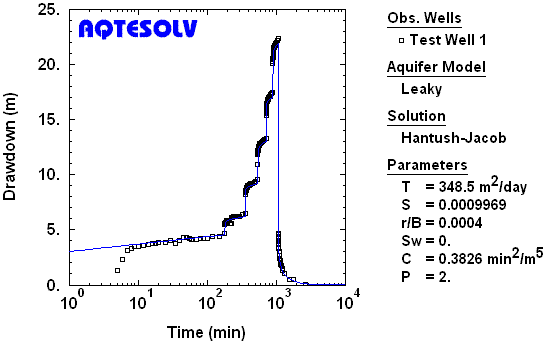
References

Hantush, M.S. and C.E. Jacob, 1955. Non-steady radial flow in an infinite leaky aquifer, Am. Geophys. Union Trans., vol. 36, no. 1, pp. 95-100.

Jacob, C.E., 1947. Drawdown test to determine effective radius of artesian well, Trans. Amer. Soc. of Civil Engrs., vol. 112, paper 2321, pp. 1047-1064.

Ramey, H.J., 1982. Well-loss function and the skin effect: A review. In: Narasimhan, T.N. (ed.) Recent trends in hydrogeology, Geol. Soc. Am., special paper 189, pp. 265-271.

Rorabaugh, M.J., 1953. Graphical and theoretical analysis of step-drawdown test of artesian well, Proc. Amer. Soc. Civil Engrs., vol. 79, separate no. 362, 23 pp.

Bear, J., 1979. Hydraulics of Groundwater, McGraw-Hill, New York, 569p.