Moench Solution for Unconfined Aquifers

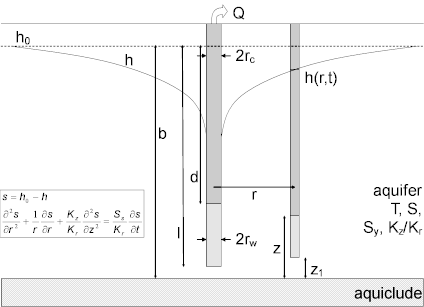
A mathematical solution by Moench (1997) is useful for determining the hydraulic properties (transmissivity, elastic storage coefficient, specific yield and vertical hydraulic conductivity) of unconfined aquifers. Analysis involves matching the solution to drawdown data collected during a pumping test. The Moench solution accounts for delayed gravity response (delayed yield), wellbore storage effects and partial penetration.

You are not restricted to constant-rate tests with the Moench solution. AQTESOLV incorporates the principle of superposition in time to simulate variable-rate and recovery tests with this method.

Wellbore storage has a distinct signature in the early-time response of a pumped well. Use the radial flow and derivative plots to detect the wellbore storage effect.

Assumptions

• aquifer has infinite areal extent
• aquifer is homogeneous, anisotropic and of uniform thickness
• aquifer potentiometric surface is initially horizontal
• pumping and observation wells are fully or partially penetrating
• aquifer is unconfined with delayed gravity response
• flow is unsteady

Equations

Moench (1997) derived an analytical solution for predicting drawdown in response to pumping in a homogeneous, anisotropic unconfined aquifer assuming partially penetrating wells, wellbore storage, wellbore skin and delayed gravity response. The solution also includes a correction for delayed observation well response.

The Laplace transform solution for dimensionless drawdown in the pumped well is as follows:

$${\overline{s}}_{wD}=\frac{2\left(A+S_w\right)}{p\left(l_D-d_D\right)\left[1+p{W}_D\left(A+S_w\right)\right]}\text{(1)}$$

The Laplace transform solution for dimensionless drawdown in a piezometer is as follows:

$${\overline{s}}_D=\frac{2E}{p\left(l_D-d_D\right)\left[1+p{W}_D\left(A+S_w\right)\right]}\text{(2)}$$

The Laplace transform solution for dimensionless drawdown in an observation well is given by the following equation:

$${\overline{s}}_D^{´}=\frac{2E^{\prime }}{p\left(l_D-d_D\right)\left[1+p{W}_D\left(A+S_w\right)\right]}\text{(3)}$$ $$A=\frac{2}{\left(l_D-d_D\right)}\sum _{n=0}^{\infty }\frac{K_0\left(q_n\right){\left\{\sin \left[{\epsilon }_n\left(1-d_D\right)\right]-\sin \left[{\epsilon }_n\left(1-l_D\right)\right]\right\}}^2}{{\epsilon }_n{q}_n{K}_1\left(q_n\right)\left[{\epsilon }_n+0.5\sin \left(2{\epsilon }_n\right)\right]}\text{(4)}$$ $$E=2\sum _{n=0}^{\infty }\frac{K_0\left(q_n{r}_D\right)\cos \left({\epsilon }_n{z}_D\right)}{q_n{K}_1\left(q_n\right)\left[{\epsilon }_n+0.5\sin \left(2{\epsilon }_n\right)\right]}$$ $$·\left\{\sin \left[{\epsilon }_n\left(1-d_D\right)\right]-\sin \left[{\epsilon }_n\left(1-l_D\right)\right]\right\}\text{(5)}$$ $$E^{\prime }=2\sum _{n=0}^{\infty }\frac{K_0\left(q_n{r}_D\right)\left[\sin \left({\epsilon }_n{z}_{D2}\right)-\sin \left({\epsilon }_n{z}_{D1}\right)\right]}{{\left(z_{D2}-z_{D1}\right){\epsilon }_{n}q}_n{K}_1\left(q_n\right)\left[{\epsilon }_n+0.5\sin \left(2{\epsilon }_n\right)\right]}$$ $$·\left\{\sin \left[{\epsilon }_n\left(1-d_D\right)\right]-\sin \left[{\epsilon }_n\left(1-l_D\right)\right]\right\}\text{(6)}$$ $$W_D=\frac{\pi r_c^2}{2\pi r_w^{2}S\left(l_D-d_D\right)}\text{(7)}$$ $$q_n=\sqrt{{\epsilon }^2{\beta }_w+p}\text{(8)}$$ $$q_n{r}_D=\sqrt{{\epsilon }^2\beta +p{r}_D^2}\text{(9)}$$ $${\beta }_w=\frac{r_w^2{K}_z}{b^2{K}_r}\text{(10)}$$ $$\beta =\frac{r^2{K}_z}{b^2{K}_r}\text{(11)}$$ $$\sigma =S/S_y\text{(12)}$$ $$\gamma ={\alpha }_{1}b{S}_y/K_z\text{(13)}$$ $$r_D=r/r_w\text{(14)}$$ $$d_D=d/b\text{(15)}$$ $$l_D=l/b\text{(16)}$$ $$z_{D1}=z_1/b\text{(17)}$$ $$z_{D2}=z_2/b\text{(18)}$$ $$t_D=\frac{Tt}{S{r}_w^2}\text{(19)}$$ $$h_D=\frac{4\pi T}{Q}\left(h_0-h\right)\text{(20)}$$

where

• ${\alpha }_1$ is an empirical constant (fitting parameter) for noninstantaneous drainage [1/T]
• $b$ is aquifer saturated thickness [L]
• $d$ is distance from water table to top of pumping well screen [L]
• $h$ is head in aquifer [L]
• $h_0$ is static head in aquifer [L]
• $K_i$ is modified Bessel function of second kind, order i
• $K_r$ is radial hydraulic conductivity of aquifer [L/T]
• $K_z$ is vertical hydraulic conductivity of aquifer [L/T]
• $l$ is distance from water table to bottom of pumping well screen [L]
• $p$ is Laplace transform variable
• $Q$ is pumping rate [L³/T]
• $r$ is radial distance from pumping well to observation well [L]
• $r_c$ is casing radius of pumping well [L]
• $r_w$ is well radius of pumping well [L]
• $s$ is drawdown [L]
• $S$ is elastic storage coefficient [dimensionless]
• $S_w$ is wellbore skin factor [dimensionless]
• $S_y$ is specific yield [dimensionless]
• $t$ is elapsed time since start of pumping [T]
• $T$ is transmissivity [L²/T]
• $z$ is elevation of piezometer above base of aquifer [L]
• $z_1$ is elevation of bottom of observation well screen above base of aquifer [L]
• $z_2$ is elevation of top of observation well screen above base of aquifer [L]

In the Laplace transform solution, $S_w$ is limited to positive values; however, using the effective well radius concept, we also may simulate a negative skin (Hurst, Clark and Brauer 1969).

If you enter a radius for downhole equipment, AQTESOLV uses the effective casing radius instead of the nominal casing radius in the equations for this solution.

The ${\epsilon }_n$ terms are roots of the following equation:

$${\epsilon }_n\tan \left({\epsilon }_n\right)=\frac{p}{\left(\sigma \beta +p/\gamma \right)}\text{ (21)}$$

Moench (1997) also included a correction for delayed water-level response in a fully or partially penetrating observation well based on the work of Black and Kipp (1977):

$${\overline{h}}_{Do}=\frac{{\overline{h}}_D}{1+W_D^{\prime }p}\text{ (22)}$$ $$W_D^{\prime }=\frac{\pi r_{co}^{2}b}{2\pi r_w^{2}S{F}^{\prime }}\text{ (23)}$$ $$F^{\prime }=\frac{L}{\ln \left(L/\left(2r_{wo}\sqrt{K_z/K_r}\right)+\sqrt{1+{\left[L/\left(2r_{wo}\sqrt{K_z/K_r}\right)\right]}^2}\right)}\text{ (24)}$$

where

• $L$ is length of well screen [L]
• $r_{co}$ is casing radius of observation well or piezometer [L]
• $r_{wo}$ is well radius of observation well or piezometer [L]

The correction is based on the quasi-steady-state flow model of Hvorslev (1951) for a slug test. AQTESOLV uses the standard definition of the shape factor given by Butler (1998) which depends on the position of the well screen in the aquifer.

Note that delayed response diminishes as $r_{co}$ approaches zero; therefore, to eliminate altogether the correction for delayed response, enter a small value for the casing radius of the observation well.

Data Requirements

• pumping and observation well locations
• pumping rate(s)
• observation well measurements (time and displacement)
• casing radius and wellbore radius for pumping well(s)
• downhole equipment radius (optional)
• partial penetration depths (optional)
• saturated thickness

Solution Options

• large-diameter pumping wells
• variable pumping rates
• multiple pumping wells
• multiple observation wells
• partially penetrating pumping and observation wells
• boundaries

Estimated Parameters

• $T$ (transmissivity)
• $S$ (elastic storage coefficient)
• $S_y$ (specific yield)
• $\beta$ or $K_z/K_r$ (hydraulic conductivity anisotropy ratio)
• $S_w$ (wellbore skin factor)
• $r\left(w\right)$ (well radius)
• $r\left(c\right)$ (casing radius)
• ${\alpha }_1$ (Moench's empirical constant for noninstantaneous drainage at the water table)

AQTESOLV displays $\beta$ for tests with a single observation well or $K_z/K_r$ for multiple observation wells.

Curve Matching Tips

• Use radial flow plots to help diagnose wellbore storage.
• Use the Cooper and Jacob (1946) solution to obtain preliminary estimates of aquifer properties.
• Match early-time data affected by wellbore storage by adjusting $r\left(c\right)$ with parameter tweaking.
• If you estimate $r\left(c\right)$ for the test well, the estimated value replaces the nominal casing radius and AQTESOLV still performs the correction for downhole equipment.
• Choose Match>Visual to perform visual curve matching using the procedure for type curve solutions.
• Use active type curves for more effective visual matching with variable-rate pumping tests.
• Select $\beta$ from the Family and Curve drop-down lists on the toolbar.
• Use parameter tweaking to perform visual curve matching and sensitivity analysis.
• Perform visual curve matching prior to automatic estimation to obtain reasonable starting values for the aquifer properties.
• Enter a large value for ${\alpha }_1$ (the drainage parameter) to achieve instantaneous drainage at the water table (Neuman's model for delayed yield).

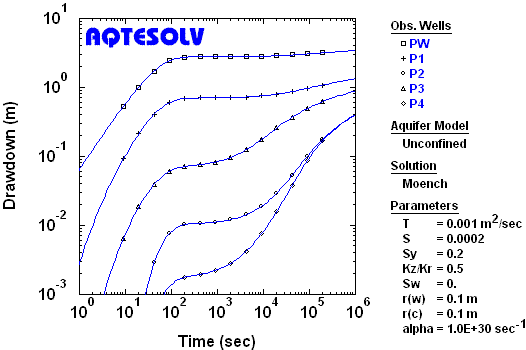
Benchmark

References

Moench, A.F., 1997. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer, Water Resources Research, vol. 33, no. 6, pp. 1397-1407.

Moench, A.F., 1998. Correction to 'Flow to a well of finite diameter in a homogeneous, anisotropic water-table aquifer,' Water Resources Research, vol. 34, no. 9, pp. 2431-2432.