Barker Solution for Nonleaky Confined Aquifers

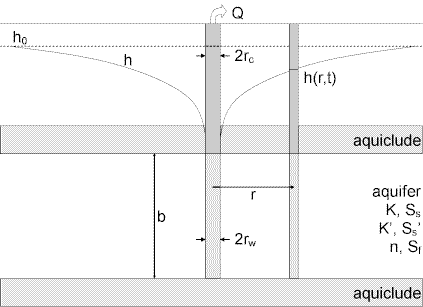
A mathematical solution by Barker (1988) known as the generalized radial flow (GRF) model is useful for determining the hydraulic properties of single- and double-porosity aquifers. Analysis involves matching the Barker solution to drawdown data collected during a pumping test.

The GRF model may be used to simulate unsteady, n-dimensional flow to a fully penetrating source in an isotropic nonleaky confined aquifer. The source is an n-dimensional sphere (projected through three-dimensional space) of finite radius ($r_w$), storage capacity ($\beta$) and skin factor ($S_w$).

You are not restricted to constant-rate tests with the Barker solution. Using the principle of superposition in time, AQTESOLV can simulate variable-rate and recovery tests with this method.

Assumptions

• aquifer has infinite extent
• aquifer is homogeneous, isotropic and of uniform extent of flow region
• potentiometric surface is initially horizontal
• aquifer is confined
• flow is unsteady
• wells are fully penetrating
• water is released instantaneously from storage with decline of hydraulic head

Equations

Barker (1988) derived a generalized radial flow model for unsteady, $n$-dimensional flow to a fully penetrating source in an isotropic nonleaky confined aquifer. The spatial dimension, $n$, determines the change in conduit area with distance from the source (Doe 1990). In a two-dimensional system ($n$=2), the source is a finite cylinder, the typical configuration for analyzing cylindrical flow to a well.

The Laplace transform solution for drawdown in the pumped well (source) is as follows:

$${\overline{h}}_w=\frac{Q\left[1+S_w{\Phi }_{\nu }\left(x\right)\right]}{p\left[p\beta \left[1+S_w{\Phi }_{\nu }\left(x\right)\right]+K{b}^{3-n}{\alpha }_n{r}_w^{n-2}{\Phi }_{\nu }\left(x\right)\right]}\text{(1)}$$

The following equation is the Laplace transform solution for drawdown in an observation well:

$$\overline{h}=\frac{Q{r}_D^{\nu }{K}_{\nu }\left(x{r}_D\right)/K_{\nu }\left(x\right)}{p\left[p\beta \left[1+S_w{\Phi }_{\nu }\left(x\right)\right]+K{b}^{3-n}{\alpha }_n{r}_w^{n-2}{\Phi }_{\nu }\left(x\right)\right]}\text{(2)}$$ $$\nu =1-n/2\text{(3)}$$ $${\lambda }^2=p{S}_s/K\text{(4)}$$ $$\mu =\lambda r_w\text{(5)}$$ $$r_D=r/r_w\text{(6)}$$ $$\Phi \left(z\right)=z{K}_{\nu -1}\left(z\right)/K_{\nu }\left(z\right)\text{(7)}$$ $${\alpha }_n=2{\pi }^{n/2}/\Gamma \left(n/2\right)\text{(8)}$$ $$\beta =\pi r_c^2\text{(9)}$$ $$x=\mu \text{(10)}$$

where

• $b$ is extent of flow region [L]
• $h$ is hydraulic head at time $t$ [L]
• $K$ is hydraulic conductivity [L/T]
• $K_{\nu }$ is modified Bessel function of second kind, order $\nu$
• $n$ is flow dimension [dimensionless]
• $p$ is the Laplace transform variable
• $Q$ is pumping rate [L³/T]
• $r$ is radial distance from pumping well to observation well [L]
• $r_c$ is casing radius [L]
• $r_w$ is well radius [L]
• $S_s$ is specific storage [dimensionless]
• $S_w$ is wellbore skin factor [dimensionless]
• $t$ is elapsed time since start of pumping [T]

The parameter $b$, the flow region extent, has a simple interpretation for integral flow dimensions.

• For $n$=1 (one-dimensional flow), $b$ is the square root of the conduit flow area (normal to the flow direction).
• For $n$=2 (two-dimensional radial flow), $b$ is the thickness of the aquifer.
• For $n$=3 (spherical flow), the parameter $b$, which is raised to the power of 3-$n$, has no significance.

For nonintegral flow dimensions, $b$ has no simple interpretation (Barker 1988).

In the Laplace transform solution, $S_w$ is limited to positive values; however, using the effective well radius concept, we also may simulate a negative skin (Hurst, Clark and Brauer 1969).

If you enter a radius for downhole equipment, AQTESOLV uses the effective casing radius instead of the nominal casing radius in the equations for this solution.

Data Requirements

• pumping and observation well locations
• pumping rate(s)
• observation well measurements (time and displacement)
• casing radius and wellbore radius for pumping well(s)
• downhole equipment radius (optional)
• extent of flow region

Solution Options

• constant or variable pumping rate with recovery
• multiple pumping wells
• multiple observation wells
• boundaries

Estimated Parameters

AQTESOLV provides visual and automatic methods for matching the Barker method to data from pumping tests and recovery tests. The estimated aquifer properties are as follows:

• $K$ (hydraulic conductivity)
• $S_s$ (specific storage)
• $n$ (flow dimension)
• $b$ (flow region extent)
• $S_w$ (dimensionless wellbore skin factor)
• $\mathrm{r(w)}$ (well radius)
• $\mathrm{r(c)}$ (nominal casing radius)

Curve Matching Tips

• Use radial flow plots to help diagnose wellbore storage.
• Use linear flow plots to help diagnose linear flow.
• Match the Cooper and Jacob (1946) solution to late-time data to obtain preliminary estimates of aquifer properties.
• Match early-time data affected by wellbore storage by adjusting $\mathrm{r(c)}$ with parameter tweaking.
• If you estimate $\mathrm{r(c)}$ for the test well, the estimated value replaces the nominal casing radius and AQTESOLV still performs the correction for downhole equipment.
• Choose Match>Visual to perform visual curve matching using the procedure for type curve solutions.
• Use active type curves for more effective visual matching with variable-rate pumping tests.
• Select values of $n$ and $S_w$ from the Family and Curve drop-down lists on the toolbar.
• Use parameter tweaking to perform visual curve matching and sensitivity analysis.
• Perform visual curve matching prior to automatic estimation to obtain reasonable starting values for the aquifer properties.

References

Barker, J.A., 1988. A generalized radial flow model for hydraulic tests in fractured rock, Water Resources Research, vol. 24, no. 10, pp. 1796-1804.

Moench, A.F., 1984. Double-porosity models for a fissured groundwater reservoir with fracture skin, Water Resources Research, vol. 20, no. 7, pp. 831-846.