Neuman-Witherspoon Solution for Confined Two-Aquifer Systems with Leakage

Description

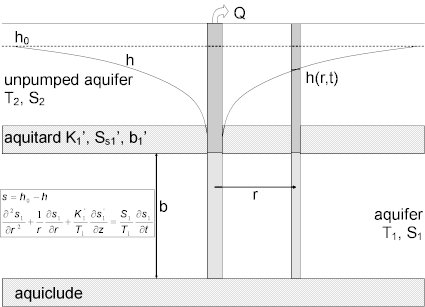
Well-aquifer configuration for Neuman and Witherspoon (1969) pumping test solution in a confined two-aquifer system with leakage

A mathematical solution by Neuman and Witherspoon (1969) is useful for determining the hydraulic properties of leaky confined aquifer systems (transmissivity and storage coefficient of the pumped aquifer; vertical hydraulic conductivity and storage coefficient of aquitard; and transmissivity and storage coefficient of the unpumped aquifer). Analysis involves matching the solution to drawdown data collected during a pumping test. Observation wells may be screened in the pumped aquifer, unpumped aquifer or aquitard.

Unlike the Hantush-Jacob (1955) and Hantush (1960) solutions for leaky confined aquifers, the Neuman and Witherspoon (1969) solution accounts for drawdown in the unpumped aquifer. Neuman and Witherspoon showed that the assumption of no drawdown in the unpumped aquifer (i.e., a constant head boundary condition) can lead to significant errors when estimating the hydraulic properties of the pumped aquifer.

Neuman-Witherspoon With RecoveryAQTESOLV provides visual and automatic methods for matching the Neuman and Witherspoon solution to pumping test and recovery test data. This easy-to-use and intuitive software promotes rapid and accurate determination of aquifer properties.

Assumptions

The following assumptions apply to the use of the Neuman and Witherspoon pumping test solution for a confined two-aquifer system with leakage:

  • aquifer has infinite areal extent
  • aquifer is homogeneous, isotropic and of uniform thickness
  • aquifer potentiometric surface is initially horizontal
  • control well is fully penetrating
  • flow to control well is horizontal
  • aquifer is leaky
  • flow is unsteady
  • water is released instantaneously from storage with decline of hydraulic head
  • diameter of control well is very small so that storage in the well can be neglected
  • aquitard has infinite areal extent, uniform vertical hydraulic conductivity and storage coefficient, and uniform thickness
  • flow in the aquitard is vertical

Solution Options

provides the following options for the Neuman and Witherspoon pumping test solution:

  • variable pumping rates
  • multiple pumping wells
  • multiple observation wells
  • boundaries

References

Neuman, S.P. and P.A. Witherspoon, 1969. Theory of flow in a confined two aquifer system, Water Resources Research, vol. 5, no. 4, pp. 803-816.

See also: solution methods, pumping tests

top